凸集合

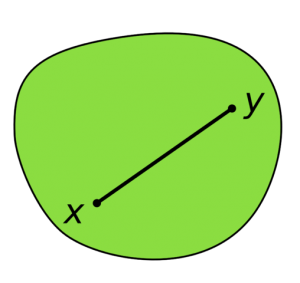
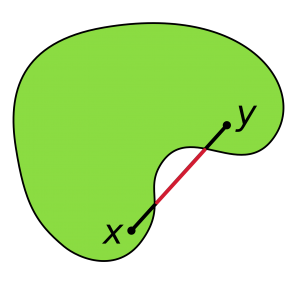
K を n 次元 Euclid 空間 Rⁿ の部分集合とします.

K の任意の2点 x，y を結ぶ線分 xy が K に含まれるとき
K は Rⁿ の凸集合であると言います：

x，y ∈ K ⇒ xy = {(1-t)x+ty  ;  0 ≤ t ≤ 1，t∈R} ⊂ K．

例えば, n-1 次元球体 D^n-1 は Rⁿ の凸集合, 立方体は R³ の凸集合です.
また, Rⁿ 自身も1つの凸集合です.
n-1 次元球面 S^n-1 は Rⁿ の凸集合ではありません.
空集合は凸集合とみなします.

平面 R² における凸集合のイメージ

凸集合

凸集合ではない

ここで気付いた人もいるかもしれませんが, ”凸” という漢字に注目して,
これを R² の部分集合と思えば明らかに凸集合ではありません.

そんな訳で凸集合について上で述べたのように説明されても
”凸” のせいでそんな感じが余りしないのは私だけでしょうか？