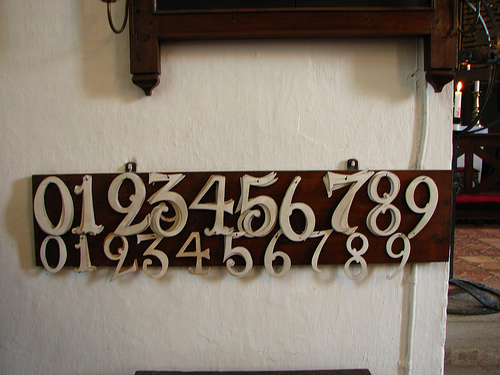全ての位が同じ数字ではない 4 桁の数は
各位の数字を並べ替えてできる最大の数から最小の数を引く計算を繰り返すと
最後には必ず 6174 になる.
この驚くべき事実は, インドの数学者 Kaprekar (カプレカ) によって発見され,
彼の名前をとって数 6174 を Kaprekar 数といいます.
試しに 1106 で計算してみました.
6110 – 0116 = 5994
9954 – 4599 = 5355
5553 – 3555 = 1998
9981 – 1899 = 8082
8820 – 0288 = 8532
8532 – 2358 = 6174
7641 – 1467 = 6174 !
尚, Kaprekar 数は 9 の倍数であることが分かります.
実際, 一般に 4 桁の数 bcad (a ≥ b ≥ c ≥ d) で考えると,
(最大数) = 1000a + 100b + 10c + d,
(最小数) = 1000d + 100c + 10b + a なので,
(最大数) – (最小数) = 999a + 90b – 90c – 999d となります.
この数は明らかに 9 の倍数ですね.