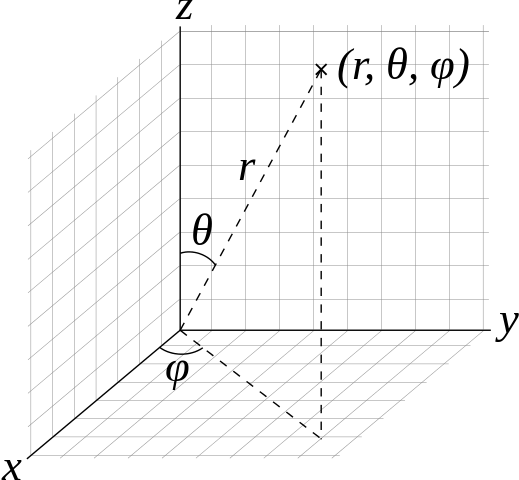
R³ 上のラプラシアン Δ = (∂²/∂x², ∂²/∂y², ∂²/∂z²) は2階微分作用素ですが, これを R³ の球面極座標
x = rsinθcosφ， y = rsinθsinφ， z = rcosθ
に変換し, r = 1 に制限したものは球面 S² 上のラプラシアンと呼びます.
これを ΔS² と書くことにします.
※ΔS² を導くために直接, 球面極座標に変換して計算すると大変なので, 先ず
x = ρcosφ， y = ρsinφ， z = z
に変換してから, もう一度
ρ = rsinθ， z = rcosθ， φ = φ
のように2次元極座標変換を行えば, 計算が割と楽になります.

R³ 上の複素係数 n 次同次多項式の空間 V_n は明らかに1つの複素ベクトル空間で,
ラプラシアン Δ の V_n への制限
Δ|V_n ： V_n → V_n-2
の kernel を U_n とおきます.

そして, U_n の元 を n 次調和多項式といい,
さらに S² に制限したものは n 次球面調和多項式と呼ばれます.

このように呼ぶと, 球面調和多項式 F(1，θ，φ) はあたかも ΔS²F = 0 となる多項式のように思えます.
しかし, 実際は ΔS²F = -n(n+1)F となることが計算で確かめられるので,
F(1，θ，φ) は ΔS² の固有多項式であり, その固有値は -n(n+1) であることが分かります.

球面調和多項式は英語の spherical harmonics の訳ですが, このような性質を持っているため誤解を招く恐れがあります.
適切な訳語であるとは余り思えないので, 英語のまま ”spherical harmonics” と言えば良いかもしれません.

次の定理を Jordan (ジョルダン) 曲線定理と呼びます.

c を平面上のループ (Jordan 曲線, 単純閉曲線とも言う) とすれば,
その補集合 R²-c は有界な部分 (内部) と有界でない部分 (外部) から成り, 2つの領域の境界は c です.
c の内部と外部からそれぞれ1点ずつをとれば, それらを結ぶ弧は必ず c と交わる.

この定理は一見明らかのように思えますが,
一般のループに対して証明するのは難しく, 位相幾何学の知識を必要とします.

いま, R² について述べましたが, R³ の場合は成り立つでしょうか？
答えは, 成り立ちません.
R³ 内のループでは内部も外部もないことは明らかでしょう.

また曲面上のループを考えると, 球面 S² 上では定理が成り立ちます.
ただ, 単連結の記事で書いたように内部・外部の区別は意味がありません.

トーラス上には定理が成立しないようなループがあります.

photo credit: Spirals and loops via photopin (license)

2次元球面 S² (我々が普段球面と思っているもの) 上にへばりついて生活している生物を想像しましょう.
つまり, その生物にとって, 球面が宇宙そのものです.

その生物を A と名付けましょう.

いま, A を囲む球面上の任意のループ (自分自身と交叉しない閉曲線) を考え, ループ上の1点 P を固定します.
A はループの内部にいますが, 点 P を固定しておいてループを連続的に変形させてどんどん広げていけば,
たちまち A はループの外部へ出てしまいます.
このことから, 球面上ではループの内部にいる A はループの外部にいるとも思えます.
逆も同様です.

ここで, ループの内部・外部という言葉を使いましたが,
それではループを赤道とすれば A は内部と外部のどちらにいるのか？
という問いが生じるので, そもそも球面上では内部・外部の区別は意味がなく,
ループは球面をただ2つの領域に分けると理解してください.

次に, 点 P を固定しておいてループを連続的に変形していくと, 点 P に縮めることが出来ます．
このとき, ループと点 P は互いにホモトープまたはホモトピックであるといいます.

一般にこのような性質が成り立つ領域は単連結であるといいます.

ちなみに, トーラスは単連結ではありません.

photo credit: Loops, I did it again. via photopin (license)