ネズミ講 (ピラミッド・スキーム) の数学的考察
Bitcoin が誕生して以来, これまで星の数ほどのデジタルアセットがブロックチェーン上で次々と誕生しています.
このデジタルアセットを用いることで, クロスボーダー送金が以前よりも格段に容易となりました.
便利になる一方で, デジタルアセットにかかるクロスボーダー犯罪 (特に詐欺) が多発しているのが現状です.
例えば, ポンジ・スキーム, HYIP (High Yield Investment Program),
違法性の高いマルチ商法 (ネットワークビジネス, ネットワークマーケティングとも言う)*1, ネズミ講などが挙げられます.
数年前の仮想通貨ブーム時は, ICO 詐欺, マイニング詐欺をよく見かけていました.
*1 マルチ商法自体は違法ではありませんが, 勧誘行為に違法性が見受けられるという意味です.
詐欺の被害にあったとしても, 仮想通貨のアドレス (アカウント) は本人確認が必要な取引所を介さない限り,
犯人の個人情報と紐付かないため, 振り込め詐欺の捜査よりも難航します.
ちなみに, 本人確認が必要な取引所を介したとしても, 途中で匿名通貨に交換していれば*2,
換金される可能性があります.
*2 よく勘違いされている事実ですが, Bitcoin は暗号化がされおらず, 匿名でもありません.
ここで, 匿名とは, Bitcoin の送信者アドレスと受信者アドレスが秘匿されているという意味です.
アドレスが個人情報と直接紐付かないというだけで, あくまでも擬似的な匿名性を有しているだけです.
さて, ここからはタイトルにある通り, 詐欺の1つであるネズミ講 (ピラミッド・スキームとも言う) について,
それが破綻する仕組みを数学的に考察します.
ネズミ講にかかる商法の会員の報酬は, 同じ商法への会員を募ることによって得られます.
会員 (親) はそれぞれ数人の新規会員を勧誘しなければなりません.
新規会員 (子) は入会費等の手数料を支払い, その一部が紹介料として勧誘者 (親) の報酬となります.
さらに, 子の会員が新規会員 (孫) を入会させると, 親と子は紹介料を得ることができます.
このように, 会員が会員を勧誘していくことで会員が増えていくさまを, ネズミの出産に例えてネズミ講と呼ばれています.
数学的に言うと, ネズミ講はある期間にネズミがどれだけ増えるかを求めるネズミ算式で, 等比級数の問題となります.
仮に, それぞれの会員が報酬を受け取るための条件として, 2 人の新規会員の勧誘が必要とします.
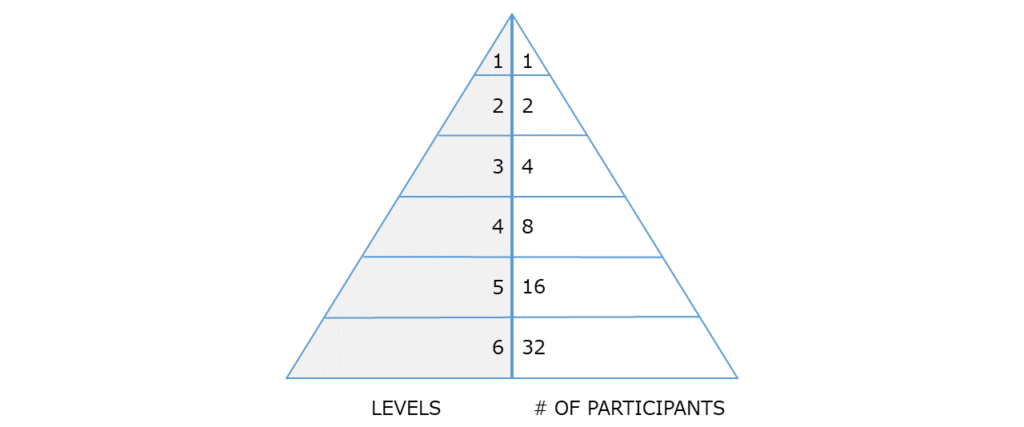
このネズミ講の首謀者を第 1 階層とすれば, 第 2 階層は 2 人, 第 3 階層は 4 人, と続いていきます.
このとき, 等比級数で表現すると, 初項が 1 (首謀者), 公比 2 (新規会員) であるから,
第 N 階層までの人数は,
1 × (1 – 2N) / (1 – 2) = 2N – 1
となります.
第 26 階層にもなると, 合計会員数が 6,700 万人となり, 第 27 階層目で日本の人口を超えてしまいます.
このようなことから, 会員が飽和してしまい破綻することになるのです.
視覚的には下図のようにピラミッド型の構造をしていることがピラミッド・スキームと言われる所以です.
逆に, 上記と同じ条件で, アメリカの人口 329,065,000 (2019年データ) を超える時点を見てみましょう.
次の式を満たす最小の階層 (自然数) N を求めます:
2N – 1 > 329065000
⇔ 2N > 329065001.
ここで, 両辺に log2 をとれば,
N > log2(329065001)
⇔ N > 28.293797350225926.
よって, 最小の階層 N は 29 となります.
ネズミ講 (ピラミッド・スキーム) の数学的考察 Read More »