Lotka-Volterra (ロトカ・ボルテラ) 方程式は次に示すように,
種内競争のない 2 種生物間における捕食系を最も簡単に表した非線型微分方程式です.
dx/dt = rx – axy,
dy/dt = bxy – cy.
ここで x, y はそれぞれ被食者と捕食者の個体数,
t は時間, r, a, b, c は正の定数です.
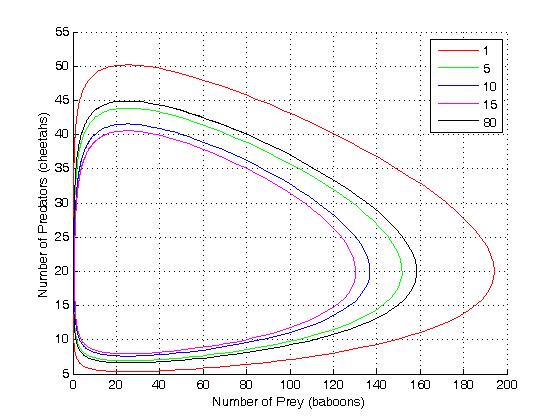
このモデルには相平面上に 2 つの平衡点 (0,0), (c/b,r/a) がありますが,
解軌道は図のように共存平衡点 (c/b,r/a) の周りを巡ることが分かります.
私が昔書いた共著論文では, Lotka-Volterra モデルの被食者・捕食者間の関係をより現実的に表したモデルを作り,
解軌道がリミットサイクルになることを Poincaré-Bendixson の定理を使って示しました.
また, 理論に基づいてシミュレーションを行い, 解の振舞いを調べました.