我々がよく知っている,
ある点を中心とした半径 r の円の面積は πr2 で与えられますが,
これは誤解を招く恐れがあります.
なぜなら, 円の定義は「ある点からの距離が等しい点の集合」だからです.
つまりこの集合は曲線 (円周という) を表しているので面積はゼロになります.
しかし, 円の面積という場合は, 円周の内部も含めて円 (円板という) とするので面積が測れます.
このように「円」といっても円周なのかそれとも円板なのか注意が必要です.
英語では, 円 (円周) を “circle”, 円板を “disk” と言って明確に言葉を使い分けています.
photo credit: Poincare lines in Firenze via photopin (license)
私の好きなボードゲームの1つが Hex です. ルールはとっても簡単.
Hex (ヘックス) とは,
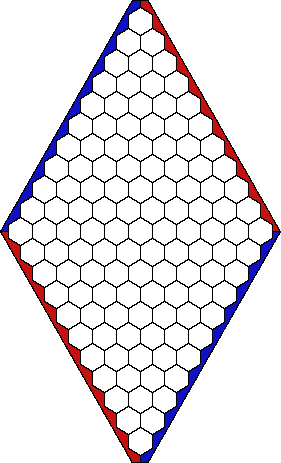
六角形が並んだ菱形のボードを使い2人で対戦するゲームです.
通常のボードのサイズは121個の六角形で構成された11×11を使用します.
しかし, Hex では任意のサイズのボードで遊ぶことができます.
Hex は1942年に Piet Hein によって考案され,
その後 Hein とは独立に John Nash も1948年に考案しました.
Nash は映画 ”A Beautiful Mind
” で有名ですね.
まず最初に2人のプレイヤーは自分の色 (赤か青) を決めます.
次に, 各プレイヤーは交互に六角形のマス目に自分の色をつけていきます.
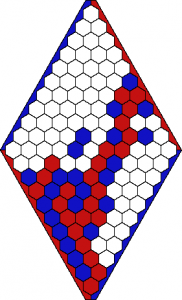
自分の色がつけられたマス目によってボードの対辺をつないだ方のプレイヤーが勝ちになります.
ただし, ボードの4隅のマス目は双方の辺に属するものとします.
赤が勝った例
Hex には幾つかの数学的性質があり
その1つが, Hex には引き分けがないということです.
これは図をみれば両者とも対辺を繋げた状態にできないことから直感的に明らかです.
この性質は David Gale によって証明され,
また彼は引き分けがないという事実は2次元の Brouwer の不動点定理と同値であることを示しています．
D. Gale, “The Game of Hex and Brouwer Fixed-Point Theorem”.
The American Mathematical Monthly 86, 818-827, 1979.
もう1つの大きな性質として, 任意のサイズ n×n のボードで
Hex は (ミスをしなければ) 先手必勝であることがJohn Nash によって証明されています.
しかし, それは存在証明なので具体的な必勝法は分かりません.
Hex のルールは簡単ですが, 一般の必勝法を見つけるのは非常に難しく
戦略は複雑なものとなっています.
上で述べた2つの数学的性質の証明はどれもシンプルなので
興味のある方は, 例えば
J. van Rijswijck, “Computer Hex: Are Bees better than Fruitflies?”
Master’s thesis. Alberta, Canada: University of Alberta, 2000.
を参照してください.
ところで, 先手必勝なるものがあると後手は不利なため, パイ・ルール (スワップ・ルールともいう) が適用されます.
つまり, 先手がマス目に色をつけた後で, 後手が「赤と青を交代」か「このまま続行」かを選択することができます.
位相幾何学で登場する有名な不動点定理について書きます.
不動点とは, 文字通り
連続写像によってある点を移したとき, 自分自身へ移る点のことをいいます：
X を位相空間とし, f：X → X を連続写像とするとき,
f(x) = x となる点 x を f の不動点 (または固定点) という.
そして Brouwer (ブラウワー) の不動点定理とは,
Dn を n 次元球体とし, f：Dn → Dn を連続写像とするとき,
f は少なくとも1つは不動点をもつ,
というものです.
低次元について直感的に理解することにします.
・n = 1 のとき：D1 = [-1，1].
正方形の向かい合う辺を結ぶ曲線 f は必ず対角線 x = f(x) と交わる
ことから分かります.
また, この場合は中間値の定理を使って証明することができます.
・n = 2 のとき：D2 は普通の円板.
座標が描かれた2枚の紙があるとします.
一方の紙はそのまま置いておき, 他方の紙をクシャクシャにして2枚の紙を重ねます.
すると, 2枚の紙が少なくとも1つの同一点で重なり合う, といった感じです.
(他方の紙を縮小して重ねても良いです)
・n = 3 のとき：D3 は普通の球体.
容器内の液体を掻き混ぜれば, 混ぜた後の点で元の位置と変わらない点が
少なくとも 1 つ存在する, という感じです.
もちろん, 元の点を掻き混ぜた後の点へ移す写像は連続としています.
数学で不動点定理といっても, 幾つもあって
例えば Brouwer の不動点定理の一般化である角谷の不動点定理は経済学で登場します.
photo credit: Crystal Ball via photopin (license)