Fulton B. Gonzalez, “Lectures on Integral Geometry and Harmonic Analysis,” COE Lecture Note Series 24, 2010.

2009年12月から2010年1月にかけて開催された,
Gonzalez 先生の集中講義の lecture note を基にして刊行されたものです.

ちなみに Gonzalez 先生は Sigurdur Helgason の弟子です.

集中講義が終わった後は, Gonzalez 先生にメールで原稿の正誤表を送ったりしていました.
原稿103ページ中, 75ページ程ざっと目を通し, 38ヶ所指摘したところは刊行時に修正されていました.
そして, lecture note の序文には, その仕事に対する功績で私の名前が掲載されています.

この講義の主な話題は Radon 変換に関するものでした.
Radon 変換は医療機器の CT スキャンに用いられているように現代社会に応用されている理論です.

現在では, Radon 変換は群論的に捉えらています.
G を局所 compact 位相群, K と H を G の閉部分群,
G, K, H, K ∩ H を unimodular とすれば,

double fibration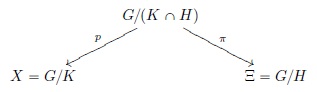

where p(g(K ∩ H))=gK, π(γ(K ∩ H))=γH

が与えられたとき,
X 上の compact 台を持つ複素数値連続函数全体 C_c(X) から
Ξ 上の函数全体への積分変換を Radon 変換と呼びます.

講義では大きく分けて, 上のような一般の Radon 変換と
次の2つの double fibration に付随する Radon 変換をやりました.

classical Radon transform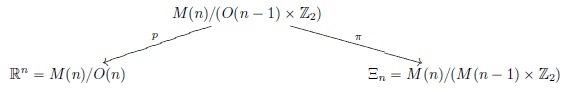

M(n): Rⁿ の等長変換群,
Ξ_n: Rⁿ の超平面全体,
Z₂: x_n=0 (x ∈ Rⁿ の第 n 成分が 0) 平面に関する鏡映により生成された群.

d-plane transform on Rⁿ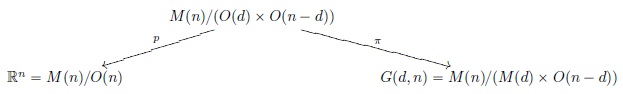

G(d, n): Rⁿ の d-plane (Rⁿ の d 次元 affine 部分空間) 全体,
つまり affine Grassmannian.

Gerrit Van Dijk, “GELFAND PAIRS AND BEYOND,” COE Lecture Note Series 11, 2008.

2008年4月から5月にかけて開催された,
van Dijk 先生の集中講義の lecture note を基にして刊行されたものです.

Outline:
1. Representations and characters of finite groups
2. Representations of compact groups
3. Characters of infinite-dimensional representations
4. Representations of compact groups (cont.)
5. Spherical harmonics
6. Compact Glefand pairs
7. Gelfand pairs
8. Generalized Gelfand pairs

Exercisesの1つに,
(SU(2), SO(2)) がコンパクト Gelfand pair であることを示す問いがありました.

この解答として, SU(2) の極大トーラス T を用いて
SU(2) = SO(2)TSO(2)
と分解すれば上手くいくと気が付いて, それに関して先生は ”Good idea!” と言って褒めて下さいました.

その解答は lecture note の中で引用されており, 私の名前が掲載されています.

私が, 角度を上手くとって SU(2) を分解したのに対して,
先生は, S³ は SU(2) の等質空間であるから,
e₁ の固定部分群を求めて分解するという方法を後で解説なされました.
このような分解の仕方はよく用いられ, 名称の付いているものもあるし,
Lie 群がある空間に推移的に作用していれば, やはりこの方法を使うのがスマートであると言えよう.