分散型合意形成と Byzantine 将軍問題

分散ネットワークシステムで昔からよく知られている問題に, Byzantine (ビザンチン) 将軍問題というものがあります.

これは分散ネットワークシステム上の合意形成にかかる問題で, 1982年に Leslie Lamport 氏らによって定式化されました:
Leslie Lamport, Robert Shostak , and Marshall Pease, The Byzantine Generals Problem, SRI International, 1982.

ちなみに Leslie Lamport 氏は, 2013年にコンピューターサイエンス分野における最高の栄誉
と言われる Turing 賞を受賞しています.
賞の名称は, エニグマ暗号機の解読者であった Alan Turing の名に由来します.

分散ネットワークシステム上では, 有限個のノードがあり, それらのノードの一部は故障していたり悪意を持っていたりします.
それらのノード間において合意形成を得るためには, 次の2つが求められます:

全ての善良ノードがメッセージ (値) について合意して終了しなければならない,
メッセージ (値) は, 善良ノードによって生成されなければならない.

Byzantine 将軍問題は, 相互に通信し合うノードにおいて, 通信および個々のノードが故障,
または故意にノードが偽の情報を伝達する可能性がある場合に, 全体として合意形成が得られるか, を問う問題です.

さて, Byzantine 将軍問題と呼ばれる由来について述べます.
これは上記で述べたシステム上の問題を, 古代東ローマ帝国 (Byzantine 帝国) の将軍に喩えたものです.

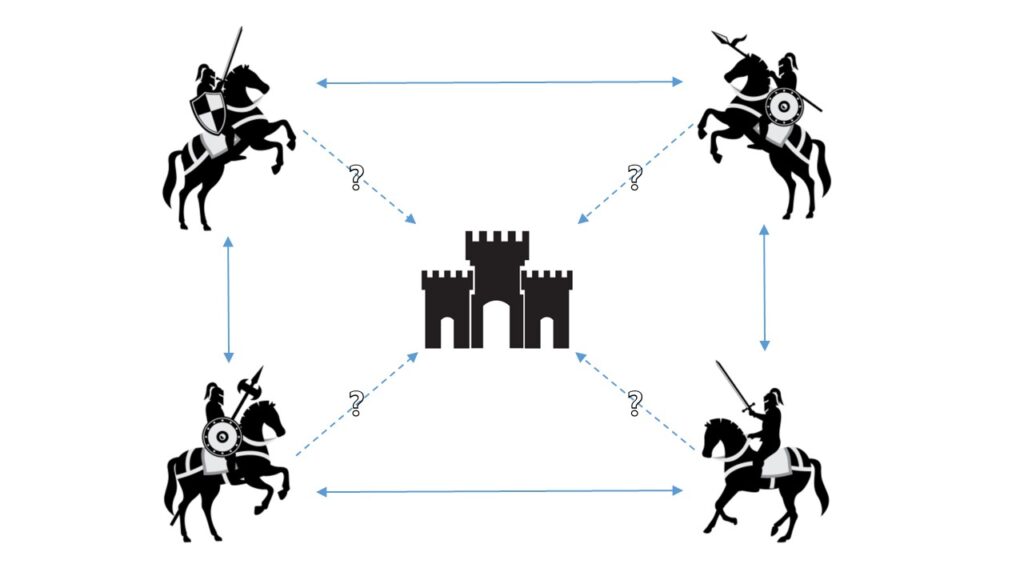
図1 Byzantine 将軍問題

Byzantine 軍は, 部隊に分かれており, それぞれが1人の将軍に率いられています.
各部隊は敵城を包囲しており, 1対1でしか互いに連絡が取れない状況を想定します.
この戦いでは, 全部隊が同時に攻め込まない限り城を落城させることができないようです.
そこで, 将軍たちは共通プランについて合意したいと考えており, 「突撃」あるいは「撤退」の判断を,
伝令を使って他の部隊へ伝えます.

しかし, 一部の将軍は裏切り者であり, 祖国に忠実な将軍たちが共通プランについて合意が形成できないように,
他の将軍から「攻撃」の情報が伝えられると, 意図的に「撤退」の情報に替えて別の将軍に伝える可能性があります.
この裏切り行為により, 一部の将軍は「突撃」と「撤退」の両方を受け取ることも考えられ,
場合によっては合意形成が得られず, 一部の部隊だけが「突撃」してしまい, Byzantine 軍は敗北することになります.

この問題のゴールは, 全ての忠実な将軍が共通プランについて合意が形成できるようにすることです.
このとき, 裏切り者の将軍の妨害により間違ったプランを採用するようなことがあってはなりません.
この問題は, 1/3 以上の将軍が裏切り者なら, 合意形成は不可能だということが証明されています.

Shapes Vectors by Vecteezy
Knight Vectors by Vecteezy
Network Stock photos by Vecteezy