Mathematics

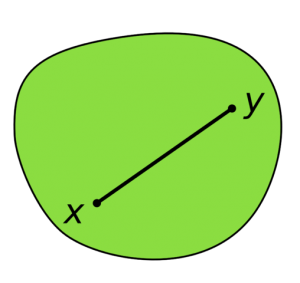
K を n 次元 Euclid 空間 Rⁿ の部分集合とします.

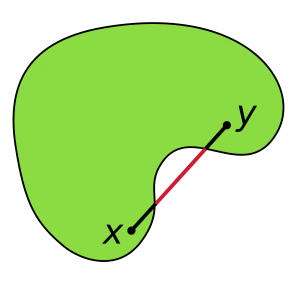
K の任意の2点 x，y を結ぶ線分 xy が K に含まれるとき
K は Rⁿ の凸集合であると言います：

x，y ∈ K ⇒ xy = {(1-t)x+ty  ;  0 ≤ t ≤ 1，t∈R} ⊂ K．

例えば, n-1 次元球体 D^n-1 は Rⁿ の凸集合, 立方体は R³ の凸集合です.
また, Rⁿ 自身も1つの凸集合です.
n-1 次元球面 S^n-1 は Rⁿ の凸集合ではありません.
空集合は凸集合とみなします.

平面 R² における凸集合のイメージ

凸集合

凸集合ではない

ここで気付いた人もいるかもしれませんが, ”凸” という漢字に注目して,
これを R² の部分集合と思えば明らかに凸集合ではありません.

そんな訳で凸集合について上で述べたのように説明されても
”凸” のせいでそんな感じが余りしないのは私だけでしょうか？

R³ 上のラプラシアン Δ = (∂²/∂x², ∂²/∂y², ∂²/∂z²) は2階微分作用素ですが, これを R³ の球面極座標
x = rsinθcosφ， y = rsinθsinφ， z = rcosθ
に変換し, r = 1 に制限したものは球面 S² 上のラプラシアンと呼びます.
これを ΔS² と書くことにします.
※ΔS² を導くために直接, 球面極座標に変換して計算すると大変なので, 先ず
x = ρcosφ， y = ρsinφ， z = z
に変換してから, もう一度
ρ = rsinθ， z = rcosθ， φ = φ
のように2次元極座標変換を行えば, 計算が割と楽になります.

R³ 上の複素係数 n 次同次多項式の空間 V_n は明らかに1つの複素ベクトル空間で,
ラプラシアン Δ の V_n への制限
Δ|V_n ： V_n → V_n-2
の kernel を U_n とおきます.

そして, U_n の元 を n 次調和多項式といい,
さらに S² に制限したものは n 次球面調和多項式と呼ばれます.

このように呼ぶと, 球面調和多項式 F(1，θ，φ) はあたかも ΔS²F = 0 となる多項式のように思えます.
しかし, 実際は ΔS²F = -n(n+1)F となることが計算で確かめられるので,
F(1，θ，φ) は ΔS² の固有多項式であり, その固有値は -n(n+1) であることが分かります.

球面調和多項式は英語の spherical harmonics の訳ですが, このような性質を持っているため誤解を招く恐れがあります.
適切な訳語であるとは余り思えないので, 英語のまま ”spherical harmonics” と言えば良いかもしれません.

次の定理を Jordan (ジョルダン) 曲線定理と呼びます.

c を平面上のループ (Jordan 曲線, 単純閉曲線とも言う) とすれば,
その補集合 R²-c は有界な部分 (内部) と有界でない部分 (外部) から成り, 2つの領域の境界は c です.
c の内部と外部からそれぞれ1点ずつをとれば, それらを結ぶ弧は必ず c と交わる.

この定理は一見明らかのように思えますが,
一般のループに対して証明するのは難しく, 位相幾何学の知識を必要とします.

いま, R² について述べましたが, R³ の場合は成り立つでしょうか？
答えは, 成り立ちません.
R³ 内のループでは内部も外部もないことは明らかでしょう.

また曲面上のループを考えると, 球面 S² 上では定理が成り立ちます.
ただ, 単連結の記事で書いたように内部・外部の区別は意味がありません.

トーラス上には定理が成立しないようなループがあります.

photo credit: Spirals and loops via photopin (license)